TheRuckSack > Land Nav Page > Lat/Lon Page

A RuckSack primer

The latitude/longitude
geographic coordinate system

By Michael A. Neiger
Copyright 2005 -- 2005-05-03

Last modified on May 3, 2005

E-mail comments or corrections to author at mneiger@hotmail.com

Return to Land Nav Page

Return to TheRuckSack home page

Article index

• Introduction
• History of lat/lon system
• Parallels of latitude
  • Introduction
  • Notable parallels
    • Arctic circle
    • Tropic of Cancer
    • Equator
    • Tropic of Capricorn
    • Antarctic circle
  • Latitudinal coordinates
• Meridians of longitude
  • Introduction
  • Notable meridians
    • Prime meridian
    • International date line
  • Longitudinal coordinates
• Calculating & plotting lat/lon coordinates on topo maps
  • Introduction
  • Drawing the lat/lon grid on maps
  • Using a lat/lon plotter
  • Commercial lat/lon plotters
  • Improvised lat/lon plotters
    • 1:20,000-scale lat/lon plotters
    • 1:24,000-scale lat/lon plotters
    • 1:25,000-scale lat/lon plotters
    • 1:50,000-scale lat/lon plotters
• Lat/lon & UTM format conversion utilities:
  • Introduction
  • Lat/lon & UTM format conversion Web sites
    • Lat/lon to lat/lon format conversions
    • Lat/lon to UTM format conversions
    • UTM to lat/lon format conversions
    • Downloadable lat/lon format conversion utilities
  • Lat/lon & UTM format conversion via GPS units
  • Lat/lon format manual conversion formulas
    • Deg-Min-Sec format to Deg-Min format
    • Deg-Min-Sec format to Deg format
    • Deg-Min format to Deg format
    • Deg-Min format to Deg-Min-Sec format
    • Deg format to Deg-Min format
    • Deg format to Deg-Min-Sec format
• Lat/lon coordinate lookup Web sites

Top
Introduction to the
latitude/longitude coordinate system

Today's latitude/longitude coordinate system is an extremely accurate and unambiguous way to describe any location on the earth’s surface. Of all the geographic coordinate systems, it is the one most often found on maps, charts, and globes. It is also the most commonly understood and often used coordinate system in existence.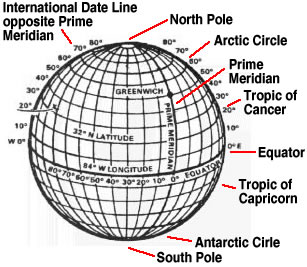

The system consists of an imaginary, two-coordinate grid overlaid on the earth’s spherical surface. The grid framework consists of an unlimited number of parallels of latitude, which are represented by the horizontal lines on a map or globe, and meridians of longitude, which are represented by the vertical lines on a map or globe.

The grid system’s zero point--0° latitude and 0° longitude--is defined as the place where the north-south running system base line, known as the prime meridian, crosses the east-west system base line, known as the equator. It is situated in the Gulf of Guinea in the Atlantic Ocean, about 375 miles south of the coast of Accra, Ghana, in western Africa.

A specific location within the latitude/longitude grid system is described by two angular descriptors, both of which are measured with respect to the center, or core, of the earth. A location’s latitudinal descriptor is represented by the angular deviation of its local parallel from the equator, or zero-degree line of latitude. A location’s longitudinal descriptor is represented by the angular deviation of its local meridian from the prime meridian, or zero-degree line of longitude.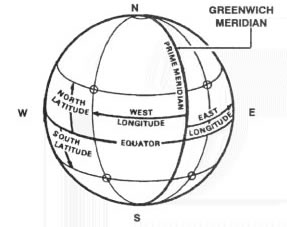

By design, no two locations on the earth’s surface can have the exact same parallel and meridian combination. In other words, every latitude/longitude coordinate combination identifies a unique and individual geographical location on the earth’s surface.

***Lat/lon diagrams adapted from the U.S. Army's Map Reading and Land Navigation Field Manual (FM 3-25.26, rev. 20 July 2001, formerly FM 21-26)

Top
An historical overview of the
latitude/longitude coordinate system

The latitude/longitude geographical coordinate system is the oldest known map-coordinate system in the world. As far back as 500 BC--some 2,500 years ago--the Greeks were using a rudimentary version to make celestial and terrestrial measurements and observations. By observing the sun, moon, planets, and stars with angle- or altitude-measuring devices, they were able approximate their terrestrial position. For seafarers of the time, accurately fixing their location while underway could mean the difference between life and death.

Through the centuries, the latitude/longitude coordinate system has evolved into an increasingly accurate means of locating one’s position on the earth’s surface and making measurements between different terrestrial locations. Along with improvements in the coordinate system, the last 2,500 years have witnessed the invention and development of various aids to navigation such as angle-measuring devices and the timekeeping instruments.

Quadrant. The medieval quadrant was probably the first angle-measuring instrument utilized for measuring latitude. As its name implies, the quadrant was configured as a quarter-of-a-circle (90 degree) arc instrument. Made of wood or brass, this portable, planispheric (flat), wedge-shaped instrument included two sights situated along one of its straight edges and a degree scale along its radius. The graduated degree scale combined with a weighted line, or plumb bob, hung from the apex, served to indicate a celestial body’s angle, or altitude, from the horizon.

In the northern hemisphere, latitude was calculated by measuring the angle between the horizon and the polar star, and then correcting this figure for the minor deviation between the polar star and the celestial north pole. In the southern hemisphere, latitude was calculated by measuring the angle between the horizon and the sun, and then correcting for the sun’s declination.

Astrolabe. The astrolabe was a medieval instrument used to measure latitude. Its name was derived from the Latin words astro, meaning star, and labio, meaning finder.This portable, angle-measuring instrument may have been invented in the 3rd century BC by Apollonius of Perga. It was a whole-circle (360 degree) planispheric, angle-measuring device constructed of brass or iron. Over the ages, it took on many forms.

In its simplest form, it consisted of two principal parts: the "mater," which was a large, circular base plate or frame graduated in degrees along its edge; and an "alidade," which was a rotating straight rule with a dual-sighting mechanism. Later models added rotating disks--such as the "rete" and the "tympan," for example--that bore celestial diagrams and charts, essentially creating a two-dimensional celestial model.

Eratosthenes and the lat/lon system. Some of the initial work on the latitude/longitude coordinate system was done during the 3rd century BC by Eratosthenes of Cyrene. While he is credited with charting lines of latitude and longitude on the earth’s surface, his charting was rudimentary and irregular at best. His system also relied on inaccurate, terrestrial-based measurements.

Hipparchus and the lat/lon system. By the 2nd century BC, Hipparchus of Nicaea had improved upon Eratosthenes’ latitude/longitude coordinate system. He is credited with plotting the lines of latitude and longitude at regular, fixed intervals. He also increased the coordinate system’s accuracy by applying trigonometry and spherical geometry, and relying upon astronomy-based measurements.

Ptolemy and the lat/lon system. In the 2nd century AD, Ptolemy of Alexandria made further improvements upon Hipparchus’ conception of the latitude/longitude system. In Geographia, a monumental, eight-volume treatise on general geography, which remained authoritative until the 15th century, Ptolemy wrote about mathematical cartography, coined the terms meridian and parallel, and cataloged a number of place names along with their corresponding latitudes and longitudes. However, inaccuracies abounded, including his estimate of Eurasia’s longitude, an error that was said to have encouraged Christopher Columbus to make his famous 1492 westward sailing voyage, which ultimately resulted in the discovery of the New World.

The magnetic compass. By the 11th century AD--if not earlier--the magnetic compass had been discovered and was in use. The first compasses were fashioned of lodestone--a naturally-occurring iron-bearing ore with magnetic properties. The lodestone was attached to the top of a splinter of wood or a piece of straw, reed, or cork, which was then floated in a container of water so it could rotate freely and orient itself in a north-south direction.

Eventually lodestone was used to magnetize a needle-shaped piece of iron or steel. By the 13th century, rotating compass needles and compass cards, balanced atop pin-like posts in bowl-shaped containers, were in use. It was not until the 15th century that compass users began to realize that their compasses did not point directly to the terrestrial north pole but to some other nearby location, which came to be known as the magnetic north pole. By the 19th century, liquid-filled compasses had replaced dry compasses.

Navigational maps and charts. While crude maps were drawn on clay tablets and animal skins as far back as 2500 BC by the ancient Babylonians, the Chinese are credited with printing the first maps during the 12th century AD.

Mercator maps. In 1569, the Mercator map was developed by Gerardus Mercator. His revolutionary maps used the Mercator projection--a technique which was named after him--to represent the earth’s three-dimensional, sphere-shaped surface on two-dimensional paper. The Mercator projection used the cylindrical projection method in which both parallels and meridians were represented as straight lines. This groundbreaking discovery allowed navigators to calculate both distance and direction from their maps.

Cross-staff. During the 16th century AD, the portable cross-staff widely replaced the astrolabe for calculating latitude. Also known as the Jacob’s staff, the cross-staff was nothing more than a graduated vertical staff with an adjustable crosspiece that allowed the user to measure the angle between the horizon and a celestial body, usually the north star or the sun.

Backstaff. By 1594, John Davis had improved upon the cross-staff with the development of the portable backstaff, or shadow-staff, which did not require the user to look directly into the sun. It was popular for nearly 150 years.

Vernier scale. In 1631, Pierre Vernier invented the graduated scale--or vernier scale--which represented a tremendous improvement over the transversals method (a geometric technique where a straight line cuts a system of other lines) of reading angular scales and linear rules. This mechanical device consisted of two parallel, sliding scales--a large main scale and a smaller auxiliary, or vernier, scale--that greatly increased the accuracy with which fractional parts or subdivisions of a single division on a fixed scale could be read.

Descartes and the lat/lon system. By the 17th century AD, Rene Descartes had further refined and systemized the latitude/longitude coordinate system. In Geometry, his famous 1637 work, Descartes laid out the principles of co-ordinate or analytical geometry and applied them to the latitude/longitude coordinate system.

Telescopic sighting mechanism. In 1640, William Gascoigne invented the telescopic sight, which greatly improved the accuracy with which a telescope could be aimed. His design combined crosshairs fashioned from spider web material with a refractor.

Meridian transit. Also known as a meridian circle, transit circle, transit instrument, transit telescope, or Roemer’s transit, the meridian transit was a non-portable, angle-measuring instrument used in astronomical observatories. Invented around 1684 by Ole Roemer, the meridian transit consisted of a refracting telescope with cross-hair sights mounted in such a way that it could only pivot in a north-south manner along the plane of the meridian. It also included a finely-graduated vertical circle for making accurate readings of a celestial body’s ascension and declination.

Octant or double-reflecting quadrant. About 1731, a portable device called the octant--which was first proposed by Sir Isaac Newton in the late 1600s--was simultaneously invented by an Englishman named John Hadley and an American named Thomas Godfrey. As its name implies, the portable octant was configured as an eighth-of-a-circle (45 degree) arc instrument. It could measure angles or altitudes of up to 90 degrees and quickly replaced the backstaff developed by John Davis in 1594.

This handheld astronomical instrument utilized two mirrors; index or vernier scales; plane or telescopic sights; and a plumb line or spirit level to measure the altitude of celestial bodies such as the moon, sun, and stars. Also known as the seaman’s reflecting quadrant, this instrument was often referred to by the surname of its inventor or the person who happened to improve upon its design (e.g., Hadley’s quadrant, Godfrey’s quadrant, etc.).

Sextant. The sextant, which had its origins in Hadley’s and Godfrey’s reflecting quadrants, was perfected around 1757 and quickly replaced the octant. As its name implies, the portable sextant was configured as a sixth-of-a-circle (60 degree) arc instrument. It could measure angles or altitudes of up to 120 degrees. Some sextants were constructed with arcs measuring 45 degrees, 72 degrees, and 90 degrees.

The sextant consisted of a frame and cross braces made of metal--often brass--or ebony wood, a rotating radial arm, an edge graduated in degrees, two mirrors--called the horizon glass and the index glass--and a sighting telescope.

Nautical almanac. In 1766, Nevil Maskelyne compiled the Nautical Almanac, the first accurate nautical tables that provided navigators with the day-to-day positions of celestial bodies necessary for accurate latitude and longitude calculations.

Marine chronometer. Despite the compilation of almanacs and tables to predict the day-to-day positions of celestial bodies and the development of "lunar-distance" techniques, accurate longitudinal readings were not possible until the 18th century when John Harrison invented a precise timekeeping instrument. Known as a portable marine chronometer, it allowed sailors to accurately tell time at sea and thereby more precisely calculate their longitude.

Harrison’s invention was motivated in large part by the British Board of Longitude, which in 1713 had posted a reward of 20,000 lira to anyone who developed a timepiece that could keep precise time while at sea. Inaccurate longitudinal calculations had been blamed for a string of deadly maritime disasters during this period. In 1728, Harrison began working on a marine clock known as timepiece No. 1. By 1761, he had perfected a marine chronometer called timepiece No. 4--a five-inch diameter pocket watch. He did not receive the entire, 20,000-lira award until King George III intervened on his behalf in 1773, just three years before the inventor’s death.

Top
Parallels of latitude

Parallels of latitude are the horizontal lines that often appear on maps, charts, and globes. They are also referred to as lines of latitude, latitude lines, or simply parallels. The word latitude--which is often abbreviated as lat.--is a Middle English word derived from the Latin terms latitudo, which meant breadth or width, and latus, which meant broad.

Parallels are imaginary, equally-spaced, rings that encircle the earth’s surface in an east-west fashion. They run perpendicular to meridians of longitude and parallel to both the equator and each other. Put another way, a line of latitude cuts across the north-south axis of the earth much like a knife cuts across the core of an onion as it is sliced.

No matter what their longitudinal coordinates, all locations on a specific parallel have exactly the same latitudinal coordinate. Following this same principle, every location on a specific meridian has a unique and individual latitudinal coordinate. While it is customary for cartographers to show only major parallels, and possibly their major subdivisions, on maps, charts, and globes, there is no set number of parallels: the number of parallels is unlimited.

Since the earth is not a perfect sphere, but is somewhat flattened near its geographic poles, the length of a degree of latitude (or distance between two parallels spaced one degree apart) varies slightly from 68.703 statute miles (110.567 kilometers) at the equator to 69.407 statute miles (111.699 kilometers) at the north and south poles.

Around the 46th parallel in Michigan's Upper Peninsula, one second of latitude equals about 100 feet (while one second of longitude equals about 69 feet).

***Lat/lon diagram adapted from the U.S. Army's Map Reading and Land Navigation Field Manual (FM 3-25.26, rev. 20 July 2001, formerly FM 21-26)

Notable parallels

Top
Arctic Circle

Located at 66 degrees, 30 minutes north latitude, the arctic circle marks the line of demarcation between the northern frigid zone, or north polar region, and the northern temperate zone. This imaginary circle around the earth also marks the point north of which the sun is not visible every day of the year. Situated about 1,624 miles from the geographic north pole, this parallel of latitude passes through Alaska, Canada, Greenland, the northern Atlantic Ocean, Norway, Sweden, Finland, Russia, and the Bering Sea.

Top
Tropic of Cancer

Located at 23 degrees, 27 minutes north latitude, the Tropic of Cancer marks the northern limit of the earth’s tropical--or torrid--zone. This imaginary line around the earth--or parallel of latitude--passes through the North Pacific Ocean, Mexico, the Gulf of Mexico, the Bahamas, the northern Atlantic Ocean, the Western Sahara, Mauritania, Mali, Algeria, Libya, Egypt, the Red Sea, Saudi Arabia, the United Arab Emirates, Oman, the Arabian Sea, India, Bangladesh, Myanmar, China, the South China Sea, and Taiwan.

Cancer. The Tropic of Cancer takes its name from the Cancer constellation, which occupies a 30-degree-segment of the 18-degree-wide zoidacal constellation--a swath of the heavens, known as the elliptic, that the sun traverses annually. The Cancer constellation is the fourth of 12 zodiacal constellations. This extremely faint, spring constellation is located in the equatorial region of the northern hemisphere, directly overhead, between Gemini and Leo. This constellation is also known as the Crab since the English term Cancer is derived from the Latin word Cancer, which means Crab.

Summer solstice. The Tropic of Cancer represents the northernmost point, north of the equator, where the sun appears directly overhead. When this occurs at noon on June 20, 21, or 22 of each year, it marks the arrival of the summer solstice and the longest day of the year in its hemisphere. The summer solstice represents the start of summer in the northern hemisphere (and winter in the southern hemisphere) and is sometimes referred to as the June solstice. The English word solstice is derived from the Latin term solstitium, which originated from the Latin terms sol and stit, meaning "sun" and "to stop or make stand," respectively, which is what the sun appears to do on that day.

***Lat/lon diagram adapted from the U.S. Army's Map Reading and Land Navigation Field Manual (FM 3-25.26, rev. 20 July 2001, formerly FM 21-26)

Top
Equator

Located at zero degrees latitude, the equator represents the imaginary line around the earth--or parallel of latitude--that lies an equal distance from both the geographic north and south poles. It serves to divide the earth into two hemispheres: the southern and northern. Measuring about 24,901 miles in length, the equator passes through the Pacific Ocean, Ecuador, Columbia, Brazil, the Atlantic Ocean, Gabon, the Congo, Zaire, Uganda, Kenya, Somalia, the Indian Ocean, and Indonesia.

Top
Tropic of Capricorn

Located at 23 degrees, 27 minutes south latitude, the Tropic of Capricorn marks the southern limit of the earth’s tropical--or torrid--zone. This imaginary line around the earth--a parallel of latitude--passes through the southern Pacific Ocean, Chile, Argentina, Paraguay, Brazil, South Atlantic Ocean, Namibia, Botswana, South Africa, Mozambique, Indian Ocean, Madagascar, Indian Ocean, and Australia.

Capricorn. The Tropic of Capricorn, or Capricornus, takes its name from the 30-degree-long Capricorn constellation, which is the tenth of 12 zodiacal constellations situated in an 18-degree-wide swath of the heavens--known as the elliptic--that the sun traverses annually. Also known as the Sea Goat or Horned Goat, this faint, autumn constellation is located in the equatorial region of the southern hemisphere, directly overhead, between Aquarius and Sagittarius. The English term Capricorn is derived from the Latin term Capricornus, which originated from the Latin terms caper and cornu, meaning "goat" and "horn," respectively.

Winter solstice. The Tropic of Capricorn represents the southernmost point, south of the equator, where the sun appears directly overhead. When this occurs at noon on December 21 or 22 of each year, it marks the arrival of the winter solstice and the shortest day of the year in the northern hemisphere. The winter solstice represents the start of winter in the northern hemisphere (and summer in the southern hemisphere) and is sometimes referred to as the December solstice. The English word solstice is derived from the Latin term solstitium, which originated from the Latin terms sol and stit, meaning "sun" and "to stop or make stand," respectively, which is what the sun appears to do on that day.

Top
Antarctic Circle

Located at 66 degrees, 30 minutes south latitude, the antarctic circle marks the line of demarcation between the southern frigid zone, or south polar region, and the southern temperate zone. This imaginary circle around the earth also marks the point south of which the sun is not visible every day of the year. Situated about 1,624 miles from the geographic south pole, this imaginary line around the earth--or parallel of latitude--passes through the ice-encrusted continent of Antartica as well as the Southern Ocean, or the Antarctic Ocean.

Top
Latitudinal coordinates

A specific location’s latitudinal coordinate is its northerly, or southerly, angular distance along the earth’s surface relative to the equator. It is measured as an arc, along a meridian of longitude, perpendicular to the equator, which is by convention the zero degree parallel.

The numerical coordinate

Latitudinal coordinates--which can range up to one-quarter of the earth’s circumference, from zero degrees (at the equator) to 90 degrees (at the north, or south, terrestrial poles)--are angles traditionally expressed in a degrees-minutes-seconds format: 45° 30’ 30.30"N. By custom, degree units are signified by the degree ° symbol; minutes are signified by the minutes ‘ symbol, a single tick mark or apostrophe; and seconds are signified by the seconds " symbol, or a double tick mark or quotation mark. In the degree-based latitude and longitude measurement system, a circle is made up of 360 degrees; a degree is made up of 60 minutes (a minute equals 1/60 of a degree); and a minute is made up of 60 seconds (a second equals 1/60 of a minute, or 1/3600 of a degree).

In addition to a "degrees, minutes, seconds" format, latitudinal coordinates are sometimes expressed in shortened forms such as a "degrees and minutes" format, where the parts of a minute are represented in a decimal-fraction form (e.g., 45° 30.5001’N), or a "degrees" format, where the parts of a degree are represented in decimal-fraction form (e.g., 45.5084166° N).

While decimal-fraction format coordinates are a common coordinate format option in Global Positioning System (GPS) units and mapping software programs, they are very cumbersome for plotting on topographic maps, especially in the field. Information on how to convert latitude/longitude coordinates from one format to another, or convert them to or from the UTM coordinate system, is discussed below.

***Lat/lon diagram adapted from the U.S. Army's Map Reading and Land Navigation Field Manual (FM 3-25.26, rev. 20 July 2001, formerly FM 21-26)

The hemispherical designator

Latitudinal coordinates are typically followed by a single letter or symbol that designates whether they are located north of the equator--in the northern hemisphere--or south of the equator--in the southern hemisphere. North latitudinal coordinates are customarily followed by either the letter "N" or the plus "+" symbol. South latitudinal coordinates are customarily followed by either the letter "S" or the minus "-" symbol.

Since the continental United States lies entirely within the northern hemisphere for latitudinal purposes, many U.S. maps and charts do not include a northern hemisphere designator with the latitudinal coordinates printed along the neatlines in the margins of the map or chart. Cartographers assume the user will know the latitudinal coordinate is in the northern hemisphere.

By convention, latitude/longitude coordinate combinations always list the latitudinal coordinate first and the longitudinal coordinate second.

Top
Meridians of longitude

Meridians of longitude are the vertical lines that often appear on maps, charts, and globes. They are also referred to as lines of longitude, longitudinal lines, meridians of longitude, geographic meridians, or simply meridians. The word longitude--which is often abbreviated as lon. or long.--is a Middle English word derived from the Latin terms longitudo, which meant length, and longus, which meant long.

Meridians are the imaginary, equally-spaced, half-circles that are drawn on the earth's surface in a north-south fashion, from pole to pole. They run perpendicular to the parallels of latitude. All meridians converge at the north and south geographic poles. Put another way, a line of longitude cuts through the north-south axis of the earth much like a knife cuts through the core of an apple when it is sliced.

No matter what their latitudinal coordinates, all locations on a specific meridian have exactly the same longitudinal coordinate. Following this same principle, every location on a specific parallel has a unique and individual longitudinal coordinate. While it is customary for cartographers to show only major meridians, and possibly their major subdivisions, on maps, charts, and globes, there is no set number of meridians: the number of meridians is unlimited.

The length of a degree of longitude (or width between two meridians spaced one degree apart) varies depending on the location and is a function of the cosine of its latitude. At the equator--or the zero parallel at zero degrees latitude--where the lines of longitude are their furthest apart, one degree of longitude measures 69.172 statue miles (111.321 kilometers). Near the middle of the Lower Peninsula of Michigan--or the 45th parallel at 45 degrees north latitude--one degree of longitude measures 48.995 statute miles (78.849 kilometers). At the north geographic pole--or the 90th parallel at 90 degrees north latitude--all the lines of longitude converge and one degree of longitude measures 0.000 statute miles (0.000 kilometers).

Around the 46th parallel in Michigan's Upper Peninsula, one second of longitude equals about 69 feet (while one second of latitude equals about 100 feet).

***Lat/lon diagram adapted from the U.S. Army's Map Reading and Land Navigation Field Manual (FM 3-25.26, rev. 20 July 2001, formerly FM 21-26)

Notable meridians

Top
The prime meridian

The prime meridian is defined as the meridian from which all of the earth’s other meridians are reckoned or measured. It is also known as the Greenwich Meridian, meridian of Greenwich, zero meridian, first meridian, standard meridian, reference meridian, or base meridian.

By modern convention, the prime meridian--the zero-degree, north-south line of longitude--is defined as the meridian that passes through the optical axis (crosshairs) of the Airy Transit Circle telescope at the old Royal Greenwich Observatory located in Greenwich, England. The coordinates of the Airy transit are 51° 28’ 38.1" north latitude and 000° 00’ 00" longitude.

Greenwich is a residential and industrial borough of east-central Greater London. It is situated along the south bank of the 210-mile-long River Thames, which is locally known as the London River.

The Royal Greenwich Observatory, originally known as the Observatory of Greenwich, was located in Greenwich from 1675 until the 1950s when light pollution from the Greater London area limited the observatory’s astronomical effectiveness and forced its relocation to Hurstmonceux Castle, a village located in England’s East Sussex County. In 1990, the observatory was moved to Cambridge where it remained operational until its closure in 1998.

Prior to 1884, the location of the prime meridian varied from country to country. Nations often designated their capital (e.g., Washington, Paris, Madrid, Copenhagen, Rome, Beijing, etc.) as the location of the prime meridian, and it became known as their national meridian. Sometimes convenient location or historic sites--such as the Canary Islands--were designated as an area’s prime meridian.

To eliminate the problems multiple prime meridians created for timekeeping, cartography, and navigation, the Washington Meridian Conference was held in Washington, D.C. in 1884. The result of this international meeting was a treaty that fixed the official location for the earth’s prime meridian as "the meridian passing through the centre of the transit instrument" at the United Kingdom’s Royal Astronomical Observatory located in Greenwich, England.

Time zones and the prime meridian

In addition to being the geographical location of the modern-day prime meridian, Greenwich, England also serves as the place from which Greenwich Mean Time (GMT)--the world timekeeping standard and basis for the world’s time zone system--is calculated. Greenwich Mean Time is also known as Universal Time.

Each of the world’s 24 time zones occupies a 15-degree slice of longitude. Time zones west of the Greenwich zone have times that are progressively earlier--one hour earlier per each time zone--the farther they are located west of the Greenwich zone. Time zones east of the Greenwich zone have times that are progressively later--one hour later per time zone--the farther they are located east of the Greenwich zone.

Put another way, every second, the earth rotates through 15 seconds of longitude; every minute, the earth rotates through 15 minutes of longitude; every hour, the earth rotates through 15 degrees of longitude; and every 24 hours, the earth rotates through 360 degrees of longitude, or one complete revolution.

***Lat/lon diagrams adapted from the U.S. Army's Map Reading and Land Navigation Field Manual (FM 3-25.26, rev. 20 July 2001, formerly FM 21-26)

Top
International Date Line

The International Date Line, sometimes simply known as the date line, is an irregular, imaginary line running between the north and south geographical poles. This north-south-running line is largely represented by the 180 degree east longitude meridian, or the 180 degree west longitude meridian, both of which are situated 180 degrees opposite the prime meridian. The current location of the International Date Line was officially agreed upon when the position of the prime meridian was established in 1884 at the Washington Meridian Conference in Washington, D.C.

While the location of the date line generally follows the 180-degree meridian, it does depart to the east or west in certain areas to prevent landmasses, islands, or archipelagos from straddling the dateline and having two different dates, a situation that would seriously disrupt an area’s daily life and commerce. Starting from the arctic circle, the International Date Line diverges eastward from the 180th meridian to avoid splitting Russia’s Siberia near it eastern border; westward to avoid splitting the Aleutian Islands from Alaska in the United States; and westward again to avoid splitting the Fiji Islands and to avoid separating New Zealand from it smaller islands.

As the world’s official date line, the 180th meridian marks the location on the earth’s surface where the date changes, where one day ends and the next day begins. This occurs when the sun is directly over the prime meridian, which is located on the opposite side of the earth at the zero degree line of longitude. Locations just west of the International Date Line are one day ahead of points just east of it.

***Lat/lon diagrams adapted from the U.S. Army's Map Reading and Land Navigation Field Manual (FM 3-25.26, rev. 20 July 2001, formerly FM 21-26)

Top
Longitudinal coordinates

A specific location’s longitudinal coordinate is its easterly or westerly angular distance along the earth’s surface relative to the prime meridian. It is measured as an arc, along a parallel of latitude, perpendicular to the prime meridian, which by modern convention is the zero degree meridian.

The numerical coordinate

Longitudinal coordinates--which can range up to one-half of the earth’s circumference, from zero degrees (at the prime meridian) to 180 degrees (at the international date line)--are angles traditionally expressed in a degrees-minutes-seconds format: 145° 30’ 30.30"W. By custom, degree units are signified by the degree ° symbol; minutes are signified by the minutes ‘ symbol, a single tick mark or apostrophe; and seconds are signified by the seconds " symbol, or a double tick mark or quotation mark. In the degree-based latitude and longitude measurement system, a circle is made up of 360 degrees; a degree is made up of 60 minutes (a minute equals 1/60 of a degree); and a minute is made up of 60 seconds (a second equals 1/60 of a minute, or 1/3600 of a degree).

In addition to a "degrees, minutes, seconds" format, latitudinal coordinates are sometimes expressed in shortened forms such as a "degrees and minutes" format, where the parts of a minute are represented in a decimal-fraction form (e.g., 145° 30.5001’W), or a "degrees" format, where the parts of a degree are represented in decimal-fraction form (e.g., 145.5084166° W).

While decimal-fraction format coordinates are a common coordinate format option in Global Positioning System (GPS) units and mapping software programs, they are very cumbersome for plotting on topographic maps, especially in the field. Information on how to convert latitude/longitude coordinates from one format to another, or convert them to or from the UTM coordinate system, is discussed below.

***Lat/lon diagram adapted from the U.S. Army's Map Reading and Land Navigation Field Manual (FM 3-25.26, rev. 20 July 2001, formerly FM 21-26)

The hemispherical designator

Longitudinal coordinates are typically followed by a single letter or symbol that designates whether they are located east of the prime meridian--in the eastern hemisphere--or west of the prime meridian--in the western hemisphere. West longitudinal coordinates are customarily followed by either the letter "W" or the plus "+" symbol. East longitudinal coordinates are customarily followed by either the letter "E" or the minus "-" symbol. Note: Some lat/lon coordinate systems use the minus symbol to designate westerly coordinates and the plus symbol to designate easterly coordinates.

Since the continental United States lies entirely within the western hemisphere for longitudinal purposes, many U.S. maps and charts do not include a western hemisphere designator with the longitudinal coordinates printed along the neatlines in the margins of the map or chart. Cartographers assume the user will know the longitudinal coordinate is in the western hemisphere.

By convention, latitude/longitude coordinate combinations always list the latitudinal coordinate first and the longitudinal coordinate second.

Top

Calculating & plotting
lat/lon coordinates on maps

Learning how to plot lat/lon coordinates--identify the specific location the coordinates refer to on a map--and calculate lat/lon coordinates--figure out what the coordinates are for a specific location on a map--can be an valuable skill for advanced-level wilderness trippers.

For example, sometimes wilderness trippers will be given coordinates in a lat/lon format only and it will be necessary to either use them as they are or convert them to another format. At other times, wilderness trippers will find themselves using maps or charts--especially NOAA nautical charts used by sea kayakers--that only include the lat/lon coordinate grid system.

On the majority of maps, the perimeter boundary lines--called neatlines--along the left and right sides and the tops and bottoms are represented by lines of longitude and lines of latitude, respectively. However, many maps, especially large-scale topographic maps suitable for wilderness land navigation, don’t come preprinted with a grid of such lines--called a graticule--across the interior of the map.

Topographic maps are often called quadrangles--or quads--because they represent four-sided polygons known as quadrilaterals. While it may not be readily apparent, a quad does not form a true rectangle--a parallelogram composed of four right angles--because, unlike the parallels of latitude that run parallel to each other as they form the top and bottom of a map, the meridians of longitude that form the left and right sides of the map are not straight lines and they don't run parallel to each other. Instead, the meridians of longitude bend ever so slightly as they converge at the poles.

Top
Drawing the lat/lon grid

Before a map can be used with the latitude/longitude geographic coordinate system, a grid of parallels and meridians should be overlaid on the map proper. Since most maps include a series of tick or hash marks--known as graticule marks--along the neatlines in all four margins, and sometimes within the interior of the map itself in the form of small crosses or plus "+" sign symbols, the user can simply draw the parallels and meridians across the surface of the map by using a pencil and a straightedge, such as an aluminum yardstick, to connect these preprinted marks.

In the field, lines of latitude and longitude can be drawn across a map by simply folding a corresponding map edge over onto the surface of the map to create an improvised straight edge.

Top
Using a lat/lon coordinate plotter

To calculate the latitude/longitude coordinates for a specific location on a map, or to plot known latitude/longitude coordinates--say from a GPS unit--on a map, a latitude/longitude plotter should be used.

Commercially manufactured latitude/longitude plotters, calibrated in minutes and seconds, can be purchased from a number of sources, some of which are listed below. Homemade plotters and improvised, field-expedient latitude/longitude plotters can also be fashioned as described below.

While it is possible to calculate or plot approximate latitudinal and longitudinal coordinates without a plotter through interpolation--estimating coordinates or their plots using a proportional, geometric technique--it is often much more complicated and time-consuming, not to mention less accurate, than using a latitude/longitude coordinate plotter.

To use a latitude/longitude coordinate plotter, simply position the device so each end of the appropriate scale is aligned between two, adjacent lines of latitude, or longitude, depending on which coordinate is being calculated or plotted. Often, especially when plotting longitudinal coordinates, the scale will have to be positioned at an angle between the lines, not perpendicularly, as is the custom when using most conventional rulers.

For Michigan, Canadian, and other North American quads, latitudinal coordinates increase from bottom to top, or from south to north; longitudinal coordinates increase from right to left, or from east to west.

The number of divisions on a latitude/longitude plotter often depends on the map scale for which it was designed. For example, The Coordinator, a commercial latitude/longitude plotter, is configured with the following scales:

• 1:24,000 plotter (7 & 9/16 inches long)--150 one-second divisions for grid lines spaced up to 2 minutes, 30 seconds apart.
• 1:25,000 plotter (7 & 1/4 inches long)--150 one-second divisions for grid lines spaced up to 2 minutes, 30 seconds apart
• 1:30,000 plotter (6 & 1/16 inches long)--150 one-second divisions for grid lines spaced up to 2 minutes, 30 seconds apart
• 1:50,000 plotter (7 & 1/4 inches long)--300 one-second divisions for grid lines spaced up to 5 minutes, 00 seconds apart
• 1:62,500 plotter (5 & 13/16 inches long)--300 one-second divisions for grid lines spaced up to 5 minutes, 00 seconds apart
• 1:63,360 plotter (5 & 3/4 inches long)--300 one-second divisions for grid lines spaced up to 5 minutes, 00 seconds apart
• 1:100,000 plotter (11 inches long)--450 two-second divisions for grid lines spaced up to 15 minutes, 00 seconds apart
• 1:250,000 plotter (4 & 3/8 inches long)--180 five-second divisions for grid lines spaced up to 15 minutes, 00 seconds apart

Once one coordinate is calculated, or plotted, depending on the case, the latitude/longitude plotter can then be repositioned to calculate, or plot, the remaining coordinate. While a single plotter works well for calculating the coordinates of a fixed position on a map, two plotters, used simultaneously--one to plot the latitudinal coordinate and one to plot the longitudinal coordinate--are handy for plotting a known coordinate--say from a GPS unit--on a map.

Since calculating and/or plotting latitudinal and longitudinal coordinates on topographical maps in the bush is a rather cumbersome and complicated process (due in large part to the non-symmetrical nature of the graticule), most experienced, long-range, wilderness trippers avoid this awkward system and instead rely on the easy-to-use Universal Transverse Mercator (UTM) coordinate system for rapid, on-the-go geographical calculations and plots.

Top
Commercial lat/lon &
UTM coordinate plotter vendors

Adventure GPS
1-888-477-4386
http://www.gps4fun.com

Ben Meadows Company
1-800-241-6401
http://www.benmeadows.com

Brunton Company
1-800-443-4871
http://www.brunton.com/
See "map quad tool"

Forestry Suppliers, Inc.
1-800-647-5368
http://www.forestry-suppliers.com

GPS Navigator Magazine.com
1-800-275-7526
http://www.gpsnavigatormagazine.com
Sells the Topo Companion

Lat.26Inc
1-800-305-0036
http://www.lat26inc.com

The Map Store
1-877-921-6277
http://www.maptown.com

Map Tools
1-650-529-9410
http://www.maptools.com

Ranger Joe's
1-800-247-4541
http://www.rangerjoes.com

Search Gear
1-800-474-2612
http://www.searchgear.com

Waypoint Enterprises
1-888-412-2600
http://www.waypoint-ent.com

 

Improvised lat/lon plotters

Top
1:20,000 (5.4’ by 8’) Ontario quads

The quad. The Ontario Ministry of Natural Resources 1:20,000-scale quad is a topographic base map published by the Province of Ontario, Canada. This 19.75-inch-wide by 19.75-inch-high map depicts 5.4 minutes of latitude and 8 minutes of longitude. Since the majority of these maps are not configured with latitudinal and longitudinal tick marks, most are not suitable for use with the latitude/longitude coordinate system.

Some of the older 1:20,000-scale quads have graticule tick marks placed at two minute--or 120 second--intervals. The neatlines along the maps’ boundaries, however, do not correspond with the parallels and meridians needed for use with the latitude/longitude coordinate system. Instead, they represent the easting and northing lines necessary for use with the Universal Transverse Mercator (UTM) system,.

Top
1:24,000 (7.5’ by 7.5’) USGS quads

The quad. The USGS 1:24,000-scale quad is the most common topographic map in Michigan. This 15.75-inch-wide by 22.75-inch-high map depicts 7.5 minutes of latitude and 7.5 minutes of longitude. Because of its 7.5-minute size, it is often referred to as a 7.5-minute quad.

Lat/lon tick marks. On the 1:24,000-scale quad, the latitude and longitude coordinate system tick marks are located on the neatlines in all four of the map’s margins. As an aid to drawing lines between these marginal tick marks, corresponding crosses, or plus "+" sign symbols, often appear between the neatlines, within the map proper. Typically, these graticule tick marks are placed at 2.5-minute--or 150 second--intervals. Since the latitude/longitude coordinate system is not symmetrical, 2.5 minutes of latitude equals about 7.5 inches while 2.5 minutes of longitude equals about 5.25 inches.

Improvising a plotter. To improvise a latitude/longitude coordinate plotter for a 1:24,000-scale quad in the field, simply cut off a 1-inch-wide by 9-inch-long, ruler-shaped piece of the map’s blank margin. Using the statute-mile scale in the map’s bottom margin, measure off and mark 30, 1/10-of-a-mile increments (which should total exactly 3 miles) along one edge of the improvised paper ruler as shown in the following diagram.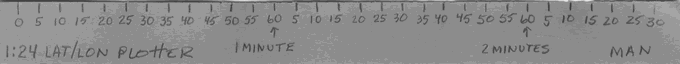

Each one of these 0.1-mile segments will correspond with 5 seconds of latitude, or longitude, depending upon which coordinate the ruler is used to measure. Similarly, 12 of these 0.1-mile segments will correspond with one minute of latitude, or longitude.

Once the ruler is marked off in 0.1-mile segments, label the first two 12-segment sections (measuring 1.2 miles and representing 60 seconds--or 1 minute--each) with the second designators of 0, 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, and 60 (the 60 would also correspond with the zero starting mark of the next segment). Once these two, 12-segment sections--measuring 1.2 miles each and representing 60 seconds (or 1 minute) each--have been marked off, mark off the remaining 6-segment section (measuring 0.6 miles and representing 30 seconds) with the second designators of 0, 5, 10, 15, 20, 25, and 30.

Using the plotter. To calculate or plot a latitudinal (or longitudinal) coordinate with this improvised ruler, simply align the zero mark on the ruler with the lower or southernmost line of latitude (or right or easternmost line of longitude) and then angle the opposite end of the ruler until the 30th mark--the 2.5-minute (150-second) mark--lines up with the adjacent upper or northern line of latitude (or the adjacent line of longitude to the left or west), which should be located 2.5 minutes away. Because of the non-symmetrical nature of the latitude/longitude coordinate system, this improvised plotter is designed to be used at an angle between two lines of latitude (or longitude), not perpendicularly.

Top
1:25,000 (7.5’ by 7.5’) USGS quads

The quad. The USGS 1:25,000-scale quad is a less common topographic map in Michigan. This 15-inch-wide by 21.75-inch-high map depicts 7.5 minutes of latitude and 7.5 minutes of longitude. Like the 1:24,000-scale quad, this map is often referred to as a 7.5-minute quad.

Lat/lon tick marks. On the 1:25,000-scale quad, the latitude and longitude coordinate system tick marks are located on the neatlines in all four of the map’s margins. As an aid to drawing lines between these marginal tick marks, corresponding crosses, or plus "+" sign symbols, often appear between the neatlines, within the map proper. Typically, these graticule tick marks are placed at 2.5-minute--or 150 second--intervals. Since the latitude/longitude coordinate system is not symmetrical, 2.5 minutes of latitude equals about 7.25 inches while 2.5 minutes of longitude equals about 5.25 inches.

Improvising a plotter. (Note: A 1:24,000-scale quad plotter will work on 1:25,000-scale quads.) To improvise a latitude/longitude coordinate plotter for a 1:24,000-scale quad in the field, simply cut off a 1-inch-wide by 9-inch-long, ruler-shaped piece of the map’s blank margin. Using the statute-mile scale in the map’s bottom margin, measure off 30, 1/10-of-a-mile increments (which should total exactly 3 miles) along one edge of the improvised paper ruler (see diagram in the 1:24,000 plotter instructions above).

Each one of these 0.1-mile segments will correspond with 5 seconds of latitude, or longitude, depending upon which coordinate the ruler is used to measure. Similarly, 12 of these 0.1-mile segments will correspond with one minute of latitude, or longitude.

Once the ruler is marked off in 0.1-mile segments, label the first two 12-segment sections (measuring 1.2 miles and representing 60 seconds--or 1 minute--each) with the second designators of 0, 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, and 60 (the 60 would also correspond with the zero starting mark of the next segment). Once these two, 12-segment sections--measuring 1.2 miles each and representing 60 seconds (or 1 minute) each--have been marked off, mark off the remaining 6-segment section (measuring 0.6 miles and representing 30 seconds) with the second designators of 0, 5, 10, 15, 20, 25, and 30.

Using the plotter. To calculate or plot a latitudinal (or longitudinal) coordinate with this improvised ruler, simply align the zero mark on the ruler with the lower or southernmost line of latitude (or right or easternmost line of longitude) and then angle the opposite end of the ruler until the 30th mark--the 2.5-minute (150-second) mark--lines up with the adjacent upper or northern line of latitude (or the adjacent line of longitude to the left or west), which should be located 2.5 minutes away. Because of the non-symmetrical nature of the latitude/longitude coordinate system, this improvised plotter is designed to be used at an angle between two lines of latitude (or longitude), not perpendicular to the edges of the map.

Top
1:50,000 (15’ by 30’) Canadian quads

The quad. The Canadian 1:50,000-scale quad is the most common topographic map in Canada. This 30-inch-wide by 21.75-inch-high map depicts 15 minutes of latitude and 30 minutes of longitude.

Lat/lon tick marks. On the 1:50,000-scale quad, the latitude and longitude coordinate system tick marks are located on the neatlines in all four of the map’s margins. There are normally no intermediate tick marks within the map proper. Typically, these graticule tick marks are placed at 5-minute--or 300 second--intervals. For convenience, the neatlines on the 1:50,000-scale quads also include a handy, checkered border that readily denotes each intermediate minute of latitude and longitude. Since the latitude/longitude coordinate system is not symmetrical, 5 minutes of latitude equals about 7.25 inches while 5 minutes of longitude equals about 5 inches.

Improvising a plotter. To improvise a latitude/longitude coordinate plotter for a 1:50,000-scale quad in the field, simply cut off a 1-inch-wide by 9-inch-long, ruler-shaped piece of the map’s blank margin. Using the statute-mile scale in the map’s bottom margin, measure off 30, 2/10-of-a-mile increments (which should total exactly 6 miles) along one edge of the improvised paper ruler (see diagram in the 1:24,000 plotter instructions above).

Each one of these 0.2-mile segments will correspond with 10 seconds of latitude, or longitude, depending upon which coordinate the ruler is used to measure. Similarly, 6 of these 0.2-mile segments will correspond with one minute of latitude, or longitude.

Once the ruler is marked off in 0.2-mile segments, label all five 6-segment sections (measuring 1.2 miles and representing 60 seconds--or 1 minute--each) with the second designators of 0, 10, 20, 30, 40, 50, and 60 (the 60 would also correspond with the zero starting mark of the next segment).

Using the plotter. To calculate or plot a latitudinal (or longitudinal) coordinate with this improvised ruler, simply align the zero mark on the ruler with the lower or southernmost line of latitude (or right or easternmost line of longitude) and then angle the opposite end of the ruler until the 30th mark--the 5-minute (300-second) mark--lines up with the adjacent upper or northern line of latitude (or the adjacent line of longitude to the left or west), which should be located 5 minutes away. Because of the non-symmetrical nature of the latitude/longitude coordinate system, this improvised plotter is designed to be used at an angle between two lines of latitude (or longitude), not perpendicularly.

Top
Lat/lon format
conversion

Converting between different formats in the latitude/longitude geographical coordinate system is a somewhat complicated process since the system uses degree-based measurements. As such, it requires making computations based not on multiples of 10, to which we are accustomed, but on multiples of 60.

For example, in the degree-based, latitude and longitude measurement system, a circle is made up of 360 degrees; a degree is made up of 60 minutes (a minute equals 1/60 of a degree); and a minute is made up of 60 seconds (a second equals 1/60 of a minute, or 1/3600 of a degree).

To make in-the-field decimal-format conversions easier, keep the following equivalents in mind:

15 minutes = 1/4 of a (hour) degree, which is 0.25 degrees
30 minutes = 1/2 of a (hour) degree, which is 0.50 degrees
45 minutes = 3/4 of a (hour) degree, which is 0.75 degrees

15 seconds = 1/4 of a minute, which is 0.25 minutes
30 seconds = 1/2 of a minute, which is 0.50 minutes
45 seconds = 3/4 of a minute, which is 0.75 minutes

Latitudinal and longitudinal coordinates in a format other than "degrees, minutes, seconds"--such as where the degrees or minutes are expressed with decimal fractions--are very difficult to plot on maps. This is one of the reasons why many experienced wilderness trippers prefer to work with the Universal Transverse Mercator (UTM) coordinate system.

Lat/lon & UTM coordinate
format conversion Web sites

Top
Lat/lon to lat/lon format converters

Montana State Library
Latitude Longitude Conversion Application
http://nris.state.mt.us/wis/location/latlong.asp

Jeep.Com
Coordinate Translation Page
http://jeeep.com/details/coord/

 

Top
Lat/lon to UTM format converters

Jeep.Com
Coordinate Translation Page
http://jeeep.com/details/coord/

Montana State Library
Graphical Locator: XY-Data (DMS) Page
http://www.esg.montana.edu/gl/xy-data2.html

U.S. Department of Commerce
National Geodetic Survey
NGS Geodetic to UTM Page
http://www.ngs.noaa.gov/cgi-bin/utm_getut.prl

Oasis.com
Coordinate Converter Page
http://www.gpsinformation.net/

 

Top
UTM to lat/lon format converters

Jeep.Com
Coordinate Translation Page
http://jeeep.com/details/coord/

Montana State Library
Graphical Locator: XY-Data (UTM) Page
http://www.esg.montana.edu/gl/xy-data3.html

U.S. Department of Commerce
National Geodetic Survey
NGS UTM to Geodetic Page
http://www.ngs.noaa.gov/cgi-bin/utm_getgp.prl

Oasis.com
Coordinate Converter Page
http://www.gpsinformation.net/

 

Top
Downloadable format conversion utilities

U.S. Department of Commerce
National Geodetic Survey
NGS Geodetic Tool Kit Page
http://www.ngs.noaa.gov/TOOLS/
Offers UTM, LAT/LON, & USNG conversion utilities

National Geospatial-Intelligence Agency
GeoTrans Translator
http://earth-info.nga.mil/GandG/geotrans/
GeoTrans utility converts wide array of coordinate formats

 

Top
Lat/lon & UTM coordinate
format conversion via a GPS unit

A Global Positioning System (GPS) unit can be used to convert latitude and longitude coordinates from one format to another. Simply set the coordinate format display (go to system setup menu) of your GPS unit to the format of your coordinates and input your coordinates. Then set the coordinate format display of your GPS unit to the desired coordinate display format and read the conversion from it.

Lat/lon to lat/lon format
manual conversion formulas

Top
DEG-MIN-SEC to DEG-MIN
Convert "degrees, minutes, seconds" format (e.g., 45° 30’ 30.31"N)
to "degrees, decimal minutes" format (e.g., 45° 30.5052’N):

Objective: convert 45° 30' 30.31"N to "degree, decimal minutes" format

Step 1: "degrees" (45°) remains unchanged

Step 2: "decimal minutes" = minutes + (seconds/60)

"decimal minutes" = 30 + (30.31/60) = 30.5052'

Result: "degree, decimal minutes" format = 45° 30.5052’N

 

Top
DEG-MIN-SEC to DEG
Convert "degrees, minutes, seconds" format (e.g., 45° 30’ 30.31"N)
to "decimal degrees" format (e.g., 45.5084194° N)

Objective: convert 45° 30’ 30.31"N to "decimal degrees" format

Step 1: "decimal degrees" = degrees + (minutes/60) + (seconds/3600)

"decimal degrees" = 45 + (30/60) + (30.31/3600) = 45.5084194°

Result: "decimal degrees" = 45.5084194°

 

Objective: convert 45° 30.5052’N to "decimal degrees" format

Step 1: "decimal degrees" = degrees + (minutes/60)

"decimal degrees" = 45 + (30.5052/60) = 45.5084°

Result: "decimal degrees" = 45.5084°

Top
DEG-MIN to DEG-MIN-SEC
Convert "degrees, decimal minutes" format (e.g., 45° 30.5052’N)
to "degrees, minutes, seconds" format (e.g., 45° 30’ 30.31"N):

Objective: convert 45° 30.5052’N to "degrees, minutes, seconds" format

Step 1: "degrees" (45°) remains unchanged

Step 2: "minutes" = MM.mmmm - 00.mmmm

"minutes" = 30.5052 - 00.5052 = 30’

Step 3: "seconds" = 00.mmmm * 60

"seconds" = 00.5052 * 60 = 30.31"

Result: "degrees, minutes, seconds" format = 45° 30' 30.31"N

Top
DEG to DEG-MIN
Convert "decimal degrees" format (e.g., 45.5084°N)
to "degrees, decimal minutes" format (e.g., 45° 30.5040’N):

Objective: convert 45.5084°N to "degrees, decimal minutes" format

Step 1: "degrees" = DD.dddd - 00.dddd

"degrees" = 45.5084 - 00.5084 = 45°

Step 2 : "decimal minutes" = 00.dddd * 60

"decimal minutes" = 00.5084 * 60 = 30.5040’

Result: "degrees, decimal minutes" format = 45° 30.5040'N

Top
DEG to DEG-MIN-SEC
Convert "decimal degrees" format (e.g., 45.5084° N)
to "degrees, minutes, seconds" format (e.g., 45° 30' 30.24"N):

Objective: convert 45.5084°N to "degrees, minutes, seconds" format

Step 1: "degrees" = DD.dddd - 00.dddd

"degrees" = 45.5084 - 00.5084 = 45°

Note: the "decimal minutes" figure must be calculated first in order to calculate the "minutes" figure

Step 2 : "decimal minutes" = 00.dddd * 60

"decimal minutes" = 00.5084 * 60 = 30.5040’

Step 3: "minutes" = MM.mmmm - 00.mmmm

"minutes" = 30.5040 - 00.5040 = 30’

Step 4: "seconds" = 00.mmmm * 60

"seconds" = 00.5040 * 60 = 30.24"

Result: "degrees, minutes, seconds" format = 45° 30' 30.24"N

Top
Lat/lon look-up Web sites

Lat/lon lookup by place-name:

USGS: Geographic Names Information System (GNIS)
http://geonames.usgs.gov/index.html
Lists latitude and longitude for 2 million place-names
and features in the United States.

Come to Bali
http://www.indo.com/distance/
Lists latitude and longitude by city place-name

Latitude/longitude lookup by zip code or place-name:

U.S. Census Bureau: U.S. Gazetteer
http://www.census.gov/cgi-bin/gazetteer
Lists latitude and longitude for zip codes or place-names

Return to top of page

Return to Land Nav Page

Return to TheRuckSack home page

In God's wilderness lies the hope of the world,
the great, fresh, unblighted, unredeemed wilderness.
 — John Muir 1838-1914, Alaska Wilderness, 1890

Content Copyright © 1984 -- 2005-05-03 by Michael A. Neiger

* All rights reserved *
No part of this Web page or this Web site protected by copyright law may be reproduced, transmitted, or used in any form--including graphic, electronic, Web, mechanical or other form--or by any means--including photocopying, recording, taping, Internet distribution, information storage retrieval system, or by other means--for any purpose, except by a reviewer, who may quote brief passages, without the prior, express, written permission of the author.

* Disclaimer *
The information contained on this Web page and this Web site are provided solely for information, illustrative, and discussion purposes. Although the author has made a sincere effort to ensure the accuracy and reliability of the information presented on this Web page and this Web site, no warranty is expressed or implied. The author assumes no responsibility or liability for any injuries, damages, losses, or other consequences that may result from the use of the information contained on this Web page and this Web site. As with any human endeavor, omissions, inaccuracies, and errors will occur on this Web page and this Web site and the author makes no representations or warranties with respect to the accuracy or completeness of the information presented or that the information presented will produce any particular result or be suitable for any particular situation, person, organization, or other entity. While corrections and revisions may or may not be made from time to time, any changes made to this Web page and this Web site are made without obligation to notify any person, organization, or other entity of any such changes. The activities and processes associated with the information contained on this Web page and this Web site are by their very nature inherently dangerous and the information presented can not take the place of good personal judgement, sound decision-making, professional training, proper equipage, adequate physical fitness, and expert guidance by trained and experienced professionals.

Comments? Suggestions? Dead links? Inaccurate info?
Contact the WebMaster at mneiger@hotmail.com

A MacroMedia DreamWeaver 4 and Fireworks 4 production

Web site URL -- http://TheRuckSack.tripod.com